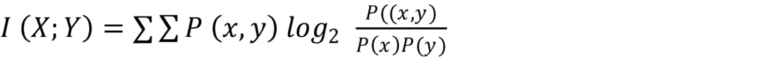Measurement of existing technical fundamentals through mutual information
True investing is an intensely intellectual endeavor. Before a Portfolio Manager (PM) can execute an investment, they must first convince themselves and then others that the rationale behind the investment is sound. The variables they use to develop their logic are of the utmost importance. These variables inevitably serve as the basis for evaluating a given Asset and therefore have the power to influence a PM’s level of confidence in the investment. If a variable is weak, it can lead to a misdiagnosis of that asset, which can lead to adverse results in a given investment. If a variable is strong, then it will indeed provide insight into the asset and hence help form a clear picture of the asset’s future. To be on the right side of this sword, it is imperative that portfolio managers properly apply quantitative reasoning, if not to their decision-making process, then certainly around it. This article introduces the theory of mutual information as a tool for asset managers to measure the predictive effectiveness of their selected variables.
Mutual Information
In information theory and statistics, mutual information is a measure of the amount of information shared between random variables (X and Y). In other words, it quantifies how much knowing one of these variables reduces uncertainty about the other, for example, if X and Y are independent, then knowing X gives no information about Y and vice versa, so the corresponding score of mutual information will be 0 .
To fully explain mutual information, it is imperative to mention the intrinsic relationship that exists between mutual information and another measure called entropy. Entropy is essentially a measure of the “uncertainty” or information content in a random variable. For example, a data set related to a financial instrument (eg, AAPL) tends to yield very high entropy scores due to potentially high levels of disorder or unpredictability within the data set. On the other hand, a binary classification problem (2 outcomes, eg coin toss) tends to yield a very low entropy score, as the data set would exhibit a higher degree of order. Relative to entropy, mutual information is the reduction of uncertainty about a variable. Therefore, regarding the output of the function (figure 1), the mutual information score is bounded below 0 (in cases of total independence between the two variables) and above the minimum of the entropy outputs between the two variables.
The mutual information between two discrete random variables (X and Y) is defined as:
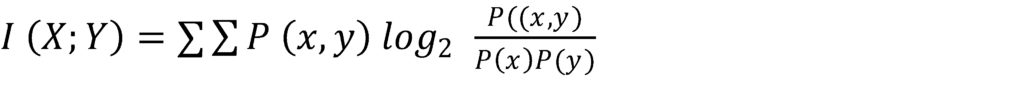
The basic ingredients of the above formula are joint probabilities [likelihood of two things occurring at the same time, denoted as P (X, Y)]as well as marginal probabilities [likelihood of individual event occurring, denoted as P (X)]. Additionally, two sums (∑) ensure that all possible combinations of the variables are included when one runs the formula, and 〖log〗_2 helps scale the mutual information score itself, making it easier to interpret and compare. A higher information score indicates strong correlations between variables, while a low or rather negligible score indicates redundancy or weak predictive power.
Mutual information rating in action
Portfolio managers can use mutual information to assess the predictive power between variables in their investment models. However, doing so requires precise problem formulation and data manipulation. This requires a PM to first and foremost adopt a perspective that is identical to the logical view of the type of mutual information explained above. In other words, PMs must mathematically model the desired outcome and map it as a variable (Y or X). Additionally, depending on the nature of the variables used in a PM’s investment process, additional functions may need to be created. Furthermore, data collection and manipulation will be imperative in this process.
Kavod Holdings (The company co-founded by the author of this article) is a small only quantitative investment company. Our approach implies that the data set for the target variable Y consists exclusively of downtrends and X represents different variables that we consider to use to predict the target variable Y. Within the given context, our main goal is to determine the degree to which a given variable X can provide: How much information about whether a downtrend (variable Y) will occur is provided by the variable X? In the table below, the mutual information score for each variable x is presented:
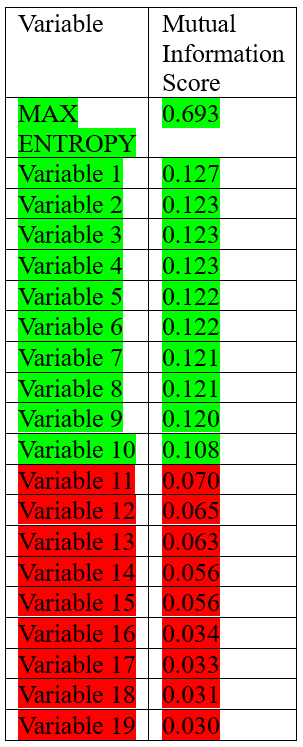
There are several paths to interpreting the mutual information score, we will examine the details in two separate approaches. This method may suit those who want to sort perhaps the information score of many different variables. A second, more efficient approach would be to use the P-value measure to interpret and compare individual scores. The P-value is a measure in statistics that quantifies the evidence against a null hypothesis. In a sense, the P value works like a lamp test, indicating the extent to which the data contradicts a proposed idea. Through the use of the p-score, PM’s will incorporate a measure of statistical significance into the variable selection process, which further increases the confidence one can justify in a particular variable. Furthermore, by limiting the P values given by each individual mutual information score for a given variable, a PM will be able to have a reliable benchmark against which to compare present and future variables. In Table 1, variables in green passed the P-value threshold while variables in red failed to pass the threshold. Therefore, red variables can be considered to have weak predictive power and therefore excluded from our investment model, while green variables, especially variable 1, would be considered to have significant mutual information scores and therefore can be used in live trading.
Performance improvement
Before incorporating the selected features into our system, our machine learning model showed an accuracy score of 0.37 (on a scale of 0 to 1) [FIG 1]. Building a capable and resilient machine learning model for any task involves many complex factors, and transactions present a unique set of challenges. Addressing these obstacles requires addressing multiple steps in various aspects of the machine learning development process. While the lower score likely stemmed from many reasons, one important factor was the inadequacy of tools—functions and formulas—within the model to accurately predict the target group.
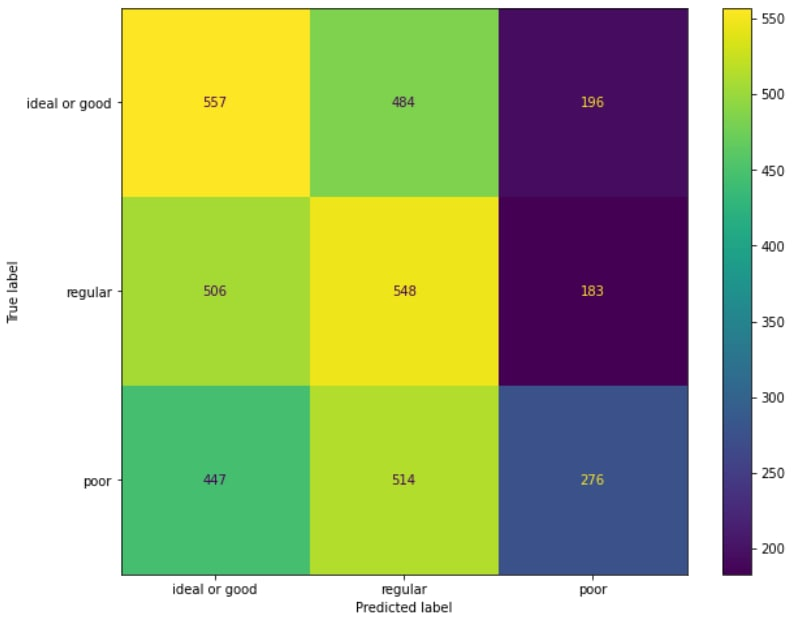
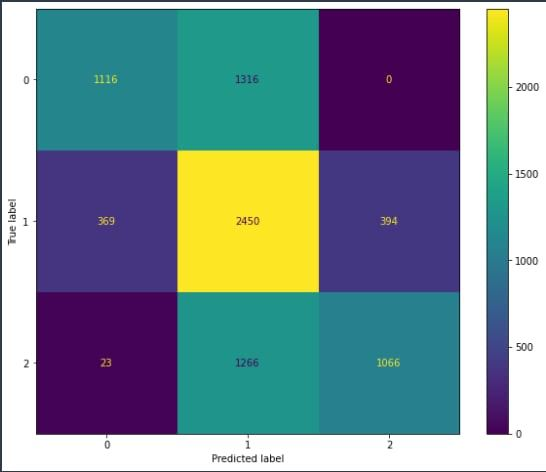
Figure 2 represents the performance of the ML model after trimming the feature list via Mutual Information Scores. In addition to the aforementioned change, we also increased the sample size for each tag, as well as troubleshooting 2 of our proprietary functions. After all implementations were completed, we saw a 0.2 increase in precision measurement from (0.37 to 0.57)
conclusion
In conclusion, mutual information can be a very powerful tool for asset managers seeking to improve their decision-making process. By understanding which variables contain substantial or rather sufficient mutual information, managers will be able to assess the strength of each variable’s influence on outcomes. In addition, managers can prioritize these variables in their decision-making process, as well as use these strong variables as benchmarks against future variables that the manager may consider adding.
About the Authors
Gabriel Kingsley-Nyinah: Gabriel Kingsley-Nyinah is the Co-Founder and CEO of Kavod Holdings. Kavod Holdings is an emerging quantitative investment firm with a distinct focus on short-term trading. In his capacity at Kavod, Gabriel has led Research and Development (R&D) initiatives, as well as overseeing commercial activities driven by sophisticated algorithms and machine learning models.
Sergey Egorov: (Master of Mathematics at the University of Rouen, France) Sergei Egorov is the head of the Research Department team at Talestorm, a software development house currently focused on LLM integration across the board, as well as at Kavod Holdings.
Looking for more strategies to read? Subscribe to our newsletter or visit our Blog or Screener.
Do you have an idea for a systematic/quantitative trading or investment strategy? Then sign up for the Quantpedia Awards 2024!
Want to learn more about the Quantpedia Premium service? Check out how Quantpedia works, our mission, and our Premium Pricing offer.
Want to learn more about the Quantpedia Pro service? Check out its description, watch videos, check out our reporting features and visit our price quote.
Looking for historical data or backtesting platforms? Check out our list of Algo Trading discounts.
Or follow us at:
Facebook Group, Facebook Page, TwitterLinkedin, Medium or Youtube
Notification toLinkedInTwitterFacebookRefer a friend