How to better estimate long-term expected returns
Niels Bohr, the Nobel laureate in physics, famously said: “Prediction is very difficult, especially if it concerns the future.” In the field of financial analysis, estimating long-term stock returns over a 10- to 20-year horizon is a formidable challenge. Despite the significant challenges in accurately forecasting market trends and economic conditions over such long periods, this task remains important for investors, portfolio managers and policymakers, some of whom often depend on these forecasts for developing effective investment strategies and policy frameworks; Evidence from today’s revised work provides valuable insights into how to improve these predictions.
The paper directly named Estimating Long-Term Expected Returns deals with the accurate estimation of long-term expected returns of equity markets, which is essential for corporate entities and individual investors alike. They investigate the ability of different input frameworks and proxies to estimate 10- and 20-year OOS returns over long historical time periods and more recent periods. They found that several approaches produce significant improvements compared to historical average model predictions. OOS-R2 can be as significant as 40% even in the most recent period, and asset allocation based on the presented model predictions can improve a portfolio’s Sharpe ratio and VaR by more than 50%.
The methodologies undertaken by the authors consist of running various frameworks and proxies used to generate long-term E(R) forecasts and comparing the performance of approaches to estimating expected returns that have been considered mostly in isolation. They show that 10- to 20-year E(R)s can be estimated in advance: Out-of-sample (OOS) forecast improvements over historical mean forecasts are as large as 40% even in the most recent period. It is important that these gains exist over a series of time periods.
The results are of interest to those who require accurate long-term forecasts of expected returns, and we particularly encourage avid readers to look at Tables 1 and 2, which provide insightful summaries of the critical findings in the paper.
Authors: Rui Ma, Ben R. Marshall, Nhut H. Nguyen, Nuttawat Visaltanachoti
Title: Estimating Long-Term Expected Returns
Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4493448
Abstract:
Estimating long-term expected returns as accurately as possible is critical. Researchers typically base their estimates on performance and growth, valuation, or a combined performance, growth, and valuation framework. We run a horse race with the skills of different frames and entry proxies in each frame to estimate 10- and 20-year out-of-sample returns over time periods of 140 years and more recent. Our results indicate that several approaches greatly outperform estimates based on historical mean benchmark returns, with mean squared error improvements exceeding 40%. Using these approaches in asset allocation decisions leads to an improvement in Sharpe ratios of over 50%.
As always we present several interesting figures and tables:
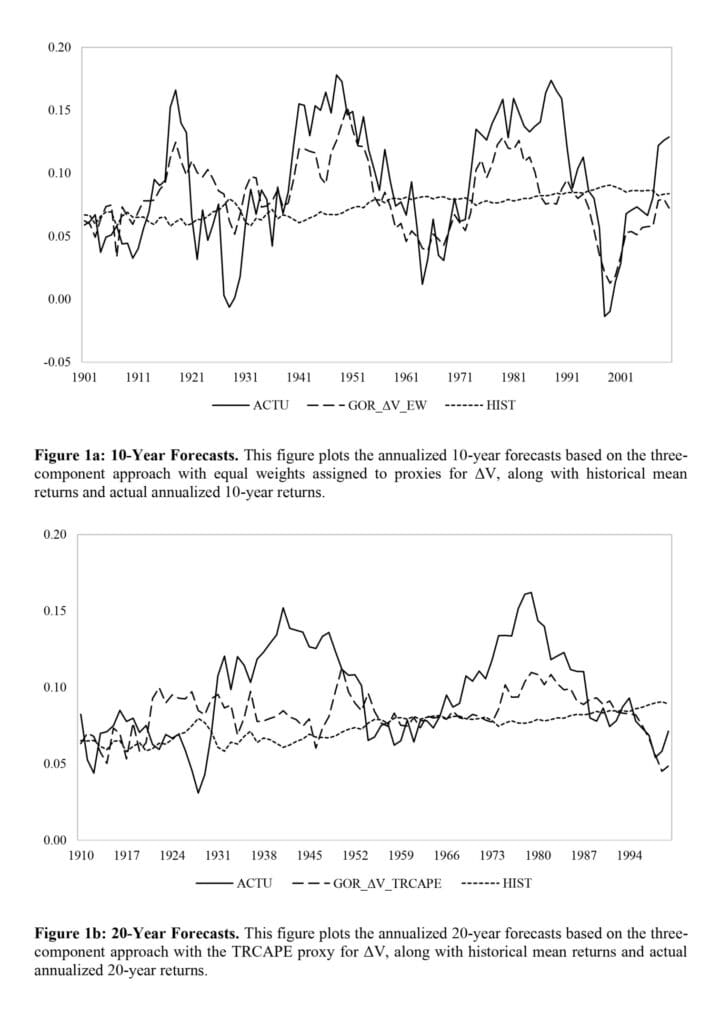
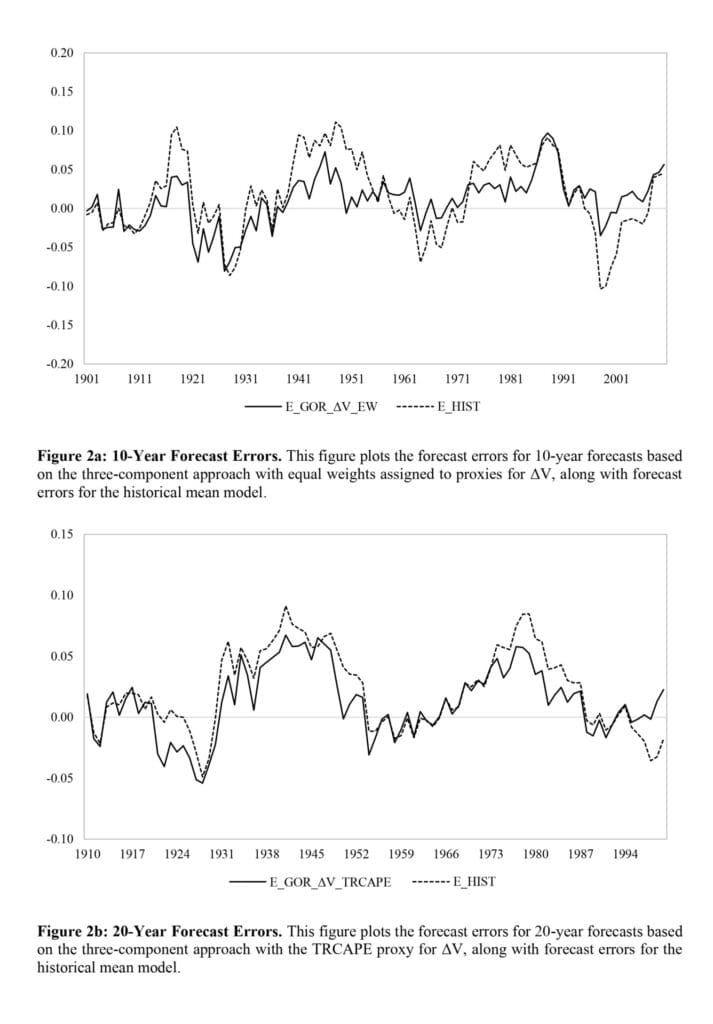
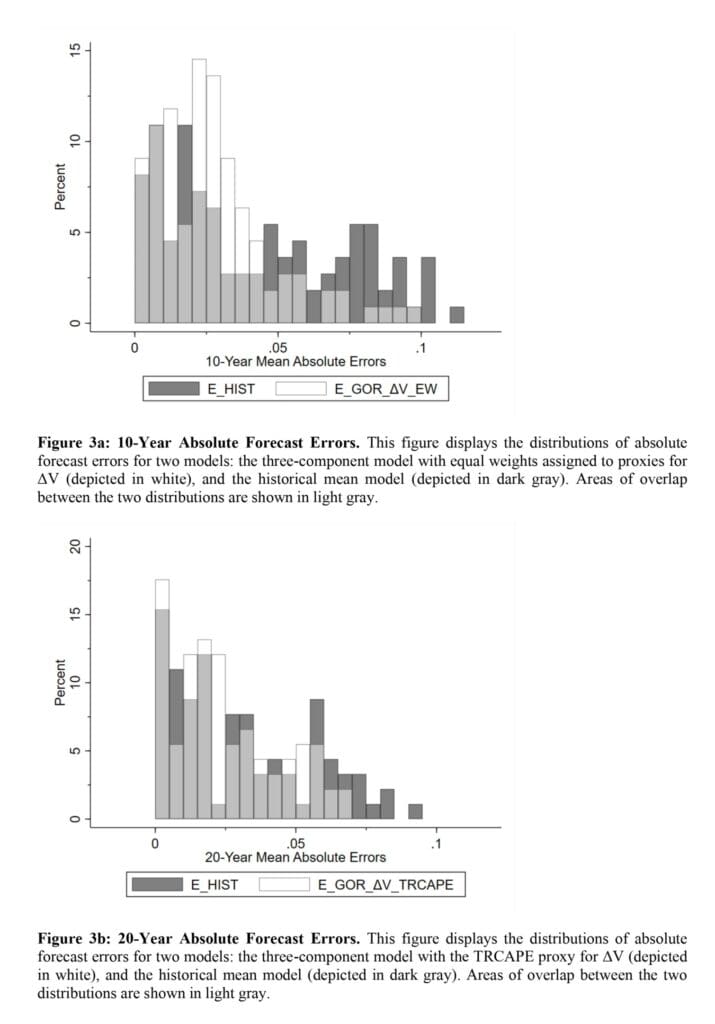
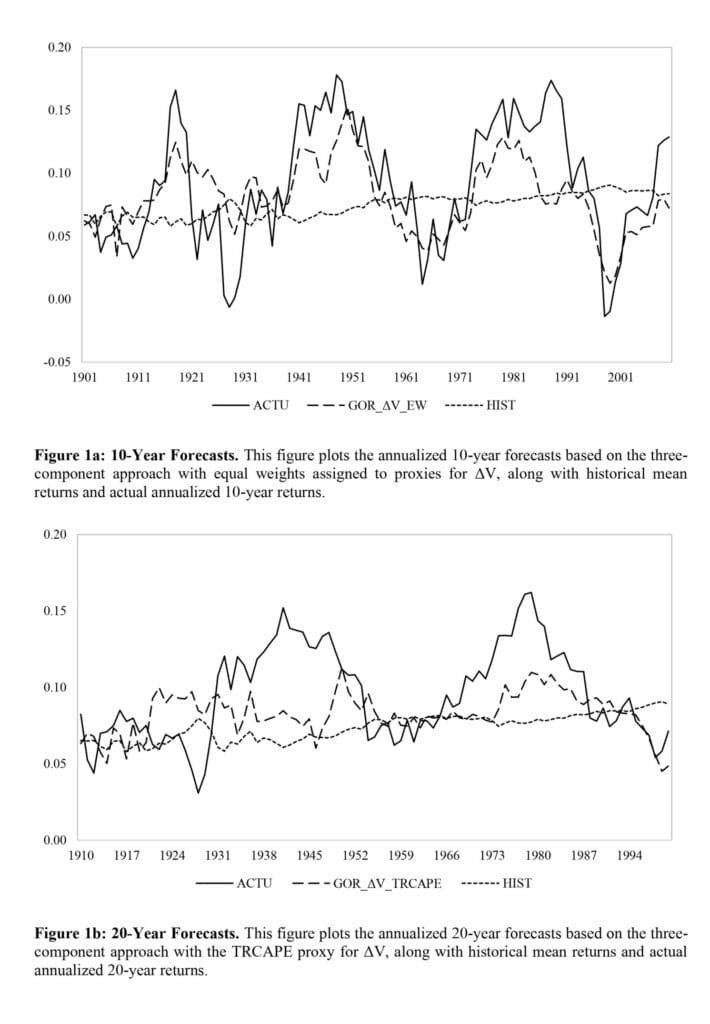
Notable quotes from the academic research paper:
“Our results show that the three-component framework is superior for 10-year forecasts, although not by a large margin. The three-component model that generates ΔV estimates based on Rintamaki’s (2023) wealth portfolio composition, denoted as VWPC, outperforms the other three-component models in predicting 10-year returns for the entire sample period from 1891 to 2020. in two more recent subsample periods, it is not statistically different from other three-component models, such as the one that assigns equal weight to four mediators for ΔV. We suggest that this latter model is superior overall as it performs better in an asset allocation setting. It causes a 34.91% decrease in MAEs and a 57.70% increase in OOS-R2 compared to the historical mean model for 10-year forecasts over the sampling period 1891–2020. Furthermore, a stock-bond portfolio with weights allocated based on these E(R) forecasts has about a 65.56% higher Sharpe ratio and a 50.06% improvement in value at risk (VaR) over the period 1891-2020. Importantly, this model also leads to improvement gains in more recent periods. Twenty-year returns are usually more difficult to predict. However, several approaches, such as the three-component model with the cyclically adjusted price-to-earnings ratio of total return (TRCAPE) significantly enhance the accuracy of these forecasts.
We contribute to several strands of the literature on the predictability of long-run returns. Fama and French (1988) use a returns-only approach and show that dividend returns explain more than 25% of the variation in two- to four-year returns. Campbell and Shiller (1998) contribute to the valuation-only literature by focusing on forecasting 10-year returns using a price-to-earnings ratio derived from average earnings over the past 10 years. They suggest that accounting for earnings fluctuations over the business cycle is important and show that this measure, commonly referred to as cyclically adjusted price-to-earnings (CAPE), is effective in predicting stock returns. Bogle (1991a, b) introduces the three-component approach and suggests that forecasts of 10-year returns give “a remarkably accurate reproduction of actual realized total returns.”
We present summary statistics in Table 1. The average annual returns are 10.66%, 11.76% and 12.27% for the periods 1872–2020, 1955–2020 and 1988–2020, respectively. Returns are negatively skewed in all three sample periods. The kurtosis is negative for the whole period, but positive in the most recent periods. In panel B, we present the geometric mean and log returns for 10-year and 20-year intervals moving forward one year at a time. It is these annual log returns that we use in our model predictions. For the 10-year period, the average annual log returns are 8.65%, 9.40% and 8.57% for the three periods, respectively, while for the 20-year period, these are 8.73%, 9, 68% and 7.55% respectively. Similarly, panel C reports the standard deviation of geometric returns and log returns for 10- and 20-year intervals moving forward one year at a time.
In Table 2, we report results for 10-year forecasts. We calculate the MAE as the average absolute difference between forecast and actual returns. We also calculate the difference in MAEs between each forecast model and the historical mean forecast.7 We measure the statistical significance of this difference using the moving block bootstrap method, which accounts for autocorrelation in the time series. The optimal block length is determined according to Patton, Politis, and White (2009). For each prediction model, we generate 1000 new bootstrap samples and report statistical significance based on the one-sided bootstrap p-value (i.e., the percentage of MAEs of the bootstrap sample prediction model that exceed the historical mean of the MAE model in the same bootstrap sample ).
The results in Table 2 show that the three-component framework is the best performing framework. For 10-year forecasts, this framework has the lowest mean MAE over the periods 1981–2020, 1955–2020, and 1988–2020. To ascertain the statistical difference between the “three-component” framework and the other three frameworks (i.e., “return only”, “Gordon” and “valuation only”), we first calculate the annual mean absolute error for each framework over of time. Using the resulting four time series, we then apply the Diebold–Mariano test (Diebold and Mariano, 1995). As shown in Appendix 3, the mean absolute error of “three components” is statistically significantly lower than “Gordon” in all three time periods and statistically significantly lower than “valuation only” and “performance only” in two of the three time periods periods. “
Looking for more strategies to read? Subscribe to our newsletter or visit our Blog or Screener.
Do you have an idea for a systematic/quantitative trading or investment strategy? Then register for Quantpedia Awards 2024!
Want to learn more about the Quantpedia Premium service? Check out how Quantpedia works, our mission, and our Premium Pricing offer.
Want to learn more about the Quantpedia Pro service? Check out its description, watch videos, check out our reporting features and visit our price quote.
Looking for historical data or backtesting platforms? Check out our list of Algo Trading discounts.
Or follow us at:
Facebook Group, Facebook Page, TwitterLinkedin, Medium or Youtube
Notification toLinkedInTwitterFacebookRefer a friend